角度/度とラジアン
canvasで角度を使う時はラジアンでなければならない。(π=パイ 円周率(3.14…))
180度 = πラジアン
※ラジアンは省力してよい
180度はπに等しい。
● 180度 = π なので1度のときのπ(ラジアン)を求めるには
π/180の計算になる。
● 180度 = π なので1ラジアンのときの度を求めるには
180/πの計算になる。
θ = (π/180) * 度
※ラジアンは省力してよい。ここではラジアンの角度をθとする。
度 → ラジアン(θ)に変換。
● 45度のラジアンを求めるには、1度が π/180 なのでそれに45をかければよい。
(π/180)*45
度 = (180/π) * ラジアン
ラジアン → 度に変換。
● 45ラジアンの度を求めるには、1ラジアンが 180/π なのでそれに45をかければよい。
(180/π)*45
角度の見方
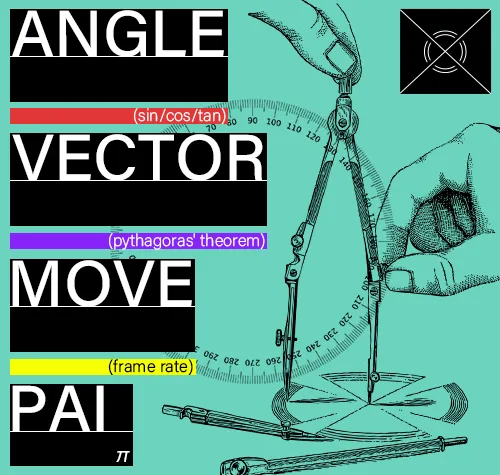
円(360度)の角度の見方。
時計の1分の場所を示す式
(Math.PI*2) × (1(分)/60) – Math.PI/2
Math.PI は180度なので倍にして360度にする。
1分は1/60になるのでかける事で度数が出る。
この時点での計算結果は「6」になるが、これは時計での見方の数字になる。
度数の始まりは時計では3の場所が0度になるので、- Math.PI/2(-90度)する。
この結果時計の1分の位置は角度上では-84度になる。
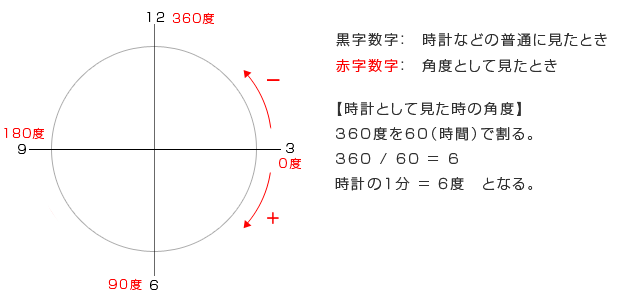
sin/cos/tan
ベクトル
基礎
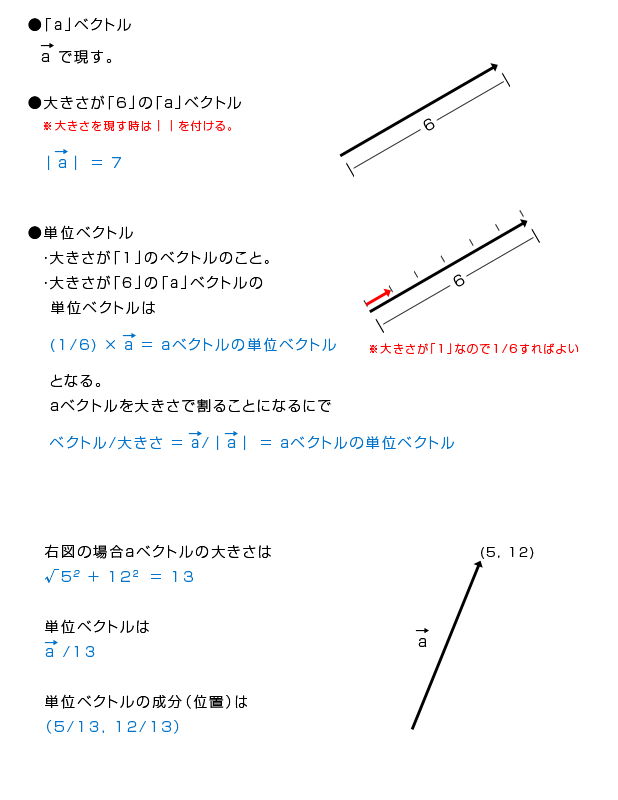
ベクトルの大きさ(ピタゴラスの定理)
ピタゴラスの定理は、直角三角形の斜辺の長さ(ベクトルの多きさ)は他の2辺の2乗の平方根に等しい。
var 変数 = Math.sqrt(Math.pow(x辺, 2) + Math.pow(y辺, 2));
・Math.sqrt・・・ルートを求める。
・Math.pow・・・二乗を求める。
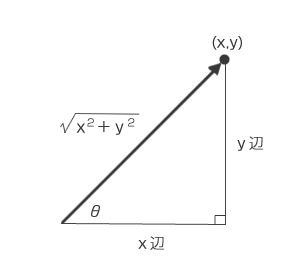
ベクトルの向き(単位ベクトル)
単位ベクトルは大きさが「1」のベクトルを表します。
//ベクトルの大きさ
var ookisa = Math.sqrt(Math.pow(x辺, 2) + Math.pow(y辺, 2));
unitVector = new Vector(); //Vectorオブジェクトのインスタンス生成
//対象ベクトルのx辺、y辺を、対象ベクトルの大きさで割る
unitVector.x = x辺 / ookisa; //ベクトルのx軸への向き
unitVector.y = y辺 / ookisa; //ベクトルのy軸への向き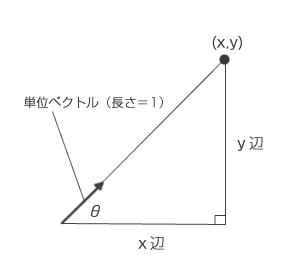
ベクトルの足し算と引き算
ベクトルの足し算、引き算は単純でただベクトル成分同士を足すまたは引くだけです。
var vector = new Vector();
//足し算
vector.x = vec1.x + vec1.y;
vector.y = vec1.y + vec1.y;
//引き算
vector.x = vec1.x - vec1.y;
vector.y = vec1.y - vec1.y;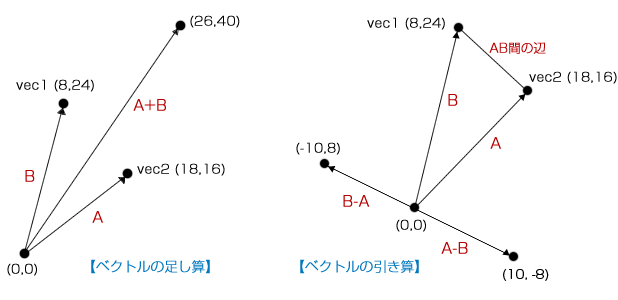
ベクトルの引き算
ベクトルからもう一方のベクトルを引くと、結果は、2つのベクトルを結んだ辺に向きが一致する3つめのベクトルになります。
上図のベクトルA-BとベクトルB-Aは平行で、またベクトルAとベクトルB間の辺ベクトルも平行です。
2つのベクトルのドット積
2つのベクトルのドット積を計算するにはベクトルの成分同士をかけ、その値を合計します。
var seki = vec1.x * vec2.x + vec1.y * vec2.y;ベクトル積はベクトルではありません。これを単なる数値を意味するスカラーと呼びます。
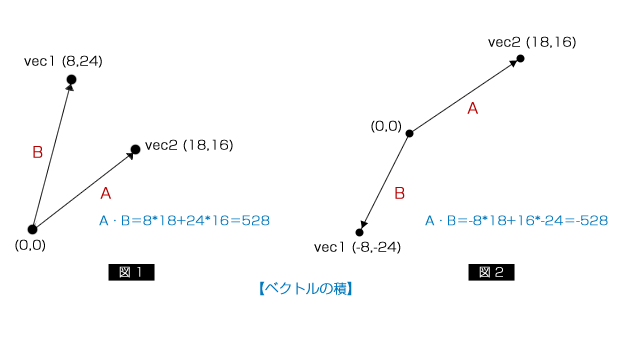
上図の「図1」のベクトルの積は528となります。
この数値が意味するのはその大きさではなく、重要なのは0より大きいということです。0より大きいということは2つのベクトルはおおよそ同じ向きを指しているということを意味します。
上図の「図2」のベクトル積は-528です。
この数値は0より小さいので2つのベクトルはおおよそ違う向きを指していることが推測できます。
2つのベクトルがおおよそ同じ向きを指しているかどうかが判定できるということは、オブジェクト同士の衝突を作用させるときに極めて重要になります。
動いているオブジェクトが動かないオブジェクトに衝突るするとき、動いている方を動かない方にあてて跳ね返させたい場合には、動いているオブジェクトが動かないオブジェクトの中心に向かうのではなく、動かないオブジェクトから離れて遠ざかるようにする必用があります。
2つのベクトルのドット積を使用するとこれが正確に実行できます。
オブジェクトの移動